When numbers are subtracted, the result is called the remainder or difference. The number subtracted is called the subtrahend; the number from which the subtrahend is subtracted is called the minuend. Subtraction is indicated by the minus sign (-).

Unlike addition, the subtraction process is neither associative nor commutative. The commutative law for addition permitted reversing the order of the addends without changing the sum. In subtraction, the subtrahend and minuend cannot be reversed.

Thus, the difference of 5 - 3 is not the same as 3 - 5. The associative law for addition permitted combining addends in any order. In subtraction, this is not allowed.

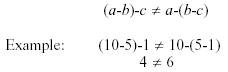
When subtracting two numbers, the subtrahend is placed under the minuend with the digits arranged in columns placing the units place under the units place, the tens column next, and so on.

Whenever the digit in the subtrahend is larger than the digit in the minuend in the same column, one place value is borrowed from the next digit to the left in the minuend. Refer to the following example.

When subtracting the units column, 6 - 8, a 10 is borrowed from the tens column. This now makes subtracting the units column 16 - 8. An 8 is placed under the units column. Next the tens column is subtracted.

A 10 was borrowed from the tens column and now 7 is subtracted from 12, not 13. This yields: 12 - 7 = 5. The 5 is placed under the tens column and the difference is 58.

This can be done for any subtraction formula. When the digit in the subtrahend column is larger than the digit in the minuend in the same column, a number from the next higher place position column is "borrowed." This reduces the higher position column by one.

Subtraction can be verified by adding the difference to the subtrahend, which should result in the minuend.