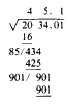If you do not have an electronic calculator, you may extract square roots arithmetically as follows:

Suppose you want to extract the square root of 2,034.01. First, divide the number into two-digit groups, working away from the decimal point. Thus set off, the number appears as follows:

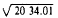
Next, find the largest number whose square can be contained in the first group, This is the number 4, whose square is 16. The 4 is the first digit of your answer. Place the 4 above the 20, and place its square (16) under the first group, thus:

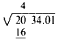
Now perform the indicated subtraction and bring down the next group to the right, thus:

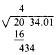
Next, double the portion of the answer already found (4, which doubled is 8), and set the result down as the first digit of a new divisor, thus:

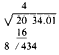
The second digit of the new divisor is obtained by a trial-and-error method. Divide the single digit 8 into the first two digits of the remainder 434 (that is, into 43) until you obtain the largest number that you can (1) add as another digit to the divisor and (2) use as a multiplier which, when multiplied by the increased divisor, will produce the largest result containable in the remainder 434. In this case, the first number you try is 43 + 8, or 5. Write this 5 after the 8 and you get 85. Multiply 85 by 5 and you get 425, which is containable in 434.

The second digit of your answer is therefore 5. Place the 5 above 34. Your computation will now look like this:

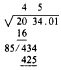
Proceed as before to perform the indicated subtraction and bring down the next group, thus:

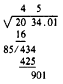
Again double the portion of the answer already found, and set the result (45 x 2, or 90) down as the first two digits of a new divisor thus:

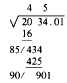
Proceed as before to determine the largest number that can be added as a digit to the divisor 90 and used as a multiplier which, when multiplied by the increased divisor, will produce a result containable in the remainder, 901. This number is obviously 1. The increased divisor is 901, and this figure, multiplied by the 1, gives a result exactly equal to the remainder 901.

The figure 1 is therefore the third and final digit in the answer, The square root of 2,034.01 is therefore 45.1

Your completed computation appears thus: