|
Area of a Triangle Figure 1-7 shows a triangle consisting of one-half
of the rectangle shown in figure 1-6. It is
obvious that the area of this triangle must equal
one-half of the area of the corresponding
rectangle, and the fact that it does can be
demonstrated by geometrical proof. Therefore,
since the formula for the area of the rectangle is
A = bh, it follows that the formula for the
triangle is A = 1/2bh.
The triangle shown in figure 1-7, because it
is half of a corresponding rectangle, contains a
right angle, and is therefore called a right triangle.
In a right triangle the dimension h corresponds
to the length of one of the sides. The triangle
shown in figure 1-8, however, is a scalene
triangle, so-called because no two sides are equal.
Classification of triangles will be discussed later
in this chapter.
Now, a perpendicular CD drawn from the
apex of the triangle (from angle C) divides the
triangle into two right triangles, DADC and
DBDC. The area of the whole triangle equals
the sum of the areas of DADC and DBDC.
The
area of DADC equals 1/2 (AD)(DC), and the
area of DBDC equals 1/2(DB)(DC). Therefore,
the area of the whole triangle equals
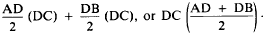
But since AD + DB = AB, it follows that the
area of the whole triangle equals
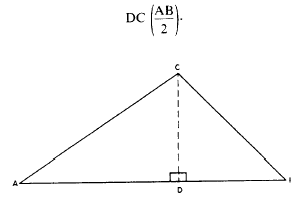
Figure 1-8.-Triangle.
The length of AB is called the base (b), and the
length of DC, the altitude (h); therefore, your for-mula
for determining the area of an oblique
triangle is again A = 1/2bh.
You must remember that in a right triangle
h corresponds to the length of one of the sides,
while in an oblique triangle it does not. Therefore,
for a right triangle with the length of the sides
given, you can determine the area by the formula
A = 1/2bh. For an oblique triangle with the
length of the sides given, you cannot use this
formula unless you can determine the value of h,
Later in this chapter you will learn trigonometric
methods of determining areas of various forms
of triangles on the basis of the length of the sides
alone.
|

