|
SETTING SLOPE STAKES. SLOPE
STAKES are driven at the intersection of
the ground and each side slope or
offset a short distance; they
indicate the earthwork limits on each
side of the center line. The minimum areas to
be cleared and grubbed extend outward about 6
ft from the slope stakes. Refer back to figure 14-31 and take a close look
at the position of the slope stakes. The
horizontal
distance of a slope stake from the center
line varies, and to determine what it is, you must
know three things.
1. The width of the roadbed, including widths of
shoulders and ditches, if any
2. The side-slope ratio (expressed in units of horizontal
run in feet per foot of vertical rise or fall)
3. The difference in elevation between the
grade for the road and the point on the natural ground
line where the slope stake will be set In
figure 14-37, view A, d is the horizontal distance
from the center line to the slope stake, W/2
is the horizontal distance from the center line to
the top of the slope, h is the difference in elevation
between the finished grade and the ground
at the slope stake, ands is the slope ratio.
The product of h x s gives the run of the slope; that
is, the horizontal distance the slope covers. The
horizontal distance (d) of the slope stake from the
center line, then, equals the sum of W/2 plus hs.
For example, suppose that W/2 is 20 ft, h is 10
ft, and the bank is a 4:1 slope. Then
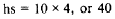
and
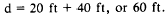
In practice, you may have to take other factors
into account, such as transverse slope or the
crossfall of the pavement (sometimes called the
crown), ditches, and so on. In figure 14-37, view
B, for example, there is a crossfall (h=) across W/2
so that the run (horizontal distance covered) of
the bank (hbs) is the product of s x hb instead of
hs, as in figure 14-31, view A. The crossfall is
usually constant and may be obtained from the typical
design sect ion shown on the plans. Figure
14-37, view C, shows a cut section in which
W/2 varies with crossfall, side slope, ditch depth,
and back slope. For example, assume that the
distance from the center line to the beginning of
the side slope is 20 ft, that the cross fall totals 1
ft, that ditch depth is 1.5 ft, and that both the side
slope and back slope ratios are 2:1. The distance
W/2, then, comprises horizontal segments
as follows:
1. From the center line to the top of the slope which
is 20 ft
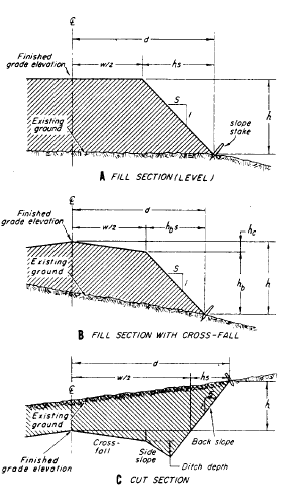
Figure 14-37.-Determining slope stake location (distance from
center line) for a proposed roadway.
2. Then to the ditch flow line, which equals the
product of slope ratio (2) times ditch depth (1.5),
or 3 ft
3. Then to the point on the back slope that is
level with the finished center line, which equals slope
ratio (2) times difference in elevation; that is,
crossfall plus ditch depth,
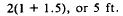
The total distance, W/2, then, is the sum of
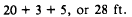
|

|

