Another ellipse is shown in the front view. This is the partly hidden and partly visible outline of the hole as it emerges through the back of the wedge. The back of the wedge is parallel to the front view plane of projection; therefore, this ellipse is the true outline of the hole on the back of the wedge. The outline is elliptical because the hole, though it is circular, is bored obliquely to the back face of the wedge.

To draw these ellipses, you could use any of the methods of drawing an accurate ellipse explained in the previous chapter on geometric construction, or you could use an ellipse template.

AUXILIARY VIEWS. In theory, there are only three regular planes of projection: the vertical, the horizonal, and the profile. Actually, it is presumed that each of these is, as it were, double; there is, for example, one vertical plane for a front view and another for a back view.

We assume, then, a total of six regular planes of projection. A projection on any one of the six is a regular view. A projection NOT on one of the regular six is an AUXILIARY VIEW.

The basic rule of dimensioning requires that a line be dimensioned only in the view in which its true length is projected and that a plane with its details be dimensioned only in the view in which its true shape is represented. To satisfy this rule, we have to create an imaginary plane that is parallel with the line or surface we want to project in its true shape. A plane of this kind that is not one of the regular planes is called an AUXILIARY PLANE.

In the upper left of figure 5-22, there is a single-view projection of a triangular block, the base of which is a rectangle. This block is presumed to be placed for multi-view projection

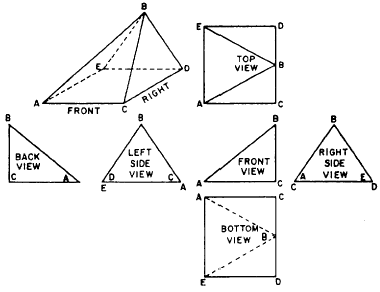
Figure 5-22.-A line oblique to all planes of projection is foreshortened in all views.

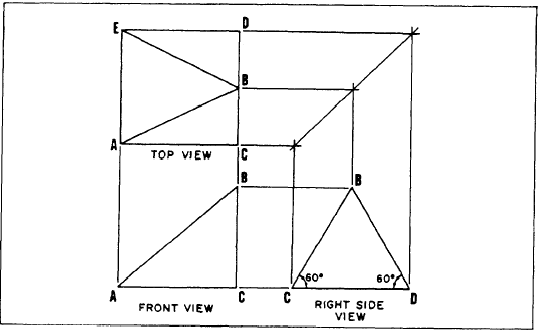
Figure 5-23.-Normal multi-view projection.

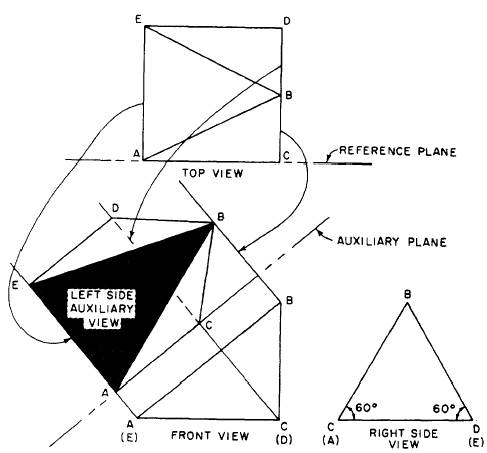
Figure 5-24.-Projection of left side auxiliary view. 

with the right side parallel to the profile plane. The block is then drawn, using all six views of multi-view projection.

By careful examination of figure 5-22, you will see that the lines AB, AE, BD and BC and the surfaces ABC, ABE, and BDE are oblique to three regular planes of projection. The lines are foreshortened and the surfaces are not shown in their true shape in any of the six normal views.

The first step in the drawing of any auxiliary view is to draw the object in normal multi-view projection, as shown in figure 5-23. A minimum of two orthographic views is necessary. The space between these views is generally greater than normal. The reason for this will become apparent. Notice in figure 5-23, in the front view, that A is the end point of line AE (top view) and C is the end point of CD.