Adding the equations would not eliminate either x or y. However, if we multiply both members of the second equation by - 1, then addition will eliminate x, as follows:

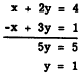
The value of x is found by substituting 1 for y in either of the original equations, as follows:

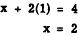
As a second example of the addition method, find the solution of the simultaneous equations

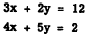
Here both x and y have unlike coefficients. The coefficients of one of the variables must be made the same, except for their signs.

The coefficients of x will be the same except signs, if both members of the first equation are multiplied by 4 and both members of the second equation by -3. Then addition will eliminate x.

Following this procedure to get the value of y, we multiply the first equation by 4 and the second equation by -3, as follows:

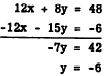
Substituting for y in the first equation to get the value of x, we have

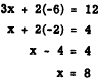
This solution is checked algebraically by substituting 8 for x and -6 for y in each of the original equations, as follows:

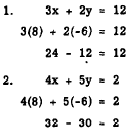
Practice problems. Use the addition method to solve the following problems:
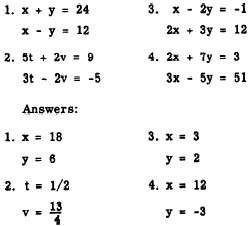