|
Other Applications
The applications of powers of 10 may be broadened
to include problems involving reciprocals and powers of products.
RECIPROCALS.-The following example illustrates the use of powers of 10 in the
formation of a reciprocal:
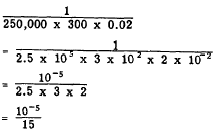
Rather than write the numerator as 0.00001, write
it as the product of two factors, one of which
may be easily divided, as follows:
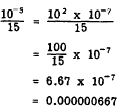
POWER OF A PRODUCT.-The following example
illustrates the use of powers of 10 in finding
the power of a product:
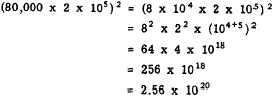
RADICALS
An expression such as 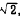 , ,  ,
or ,
or 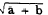 that
exhibits a radical sign, is referred to as a RADICAL.
We have already worked with radicals in the form of fractional exponents, but it
is also frequently necessary to work with them
in the radical form. The word "radical" is
derived from the Latin word "radix," which means "root."
The word "radix" itself is more often used
in modern mathematics to refer to the base of
a number system, such as the base 2 in the
binary system. However, the word "radical" is
retained with its original meaning of "root." that
exhibits a radical sign, is referred to as a RADICAL.
We have already worked with radicals in the form of fractional exponents, but it
is also frequently necessary to work with them
in the radical form. The word "radical" is
derived from the Latin word "radix," which means "root."
The word "radix" itself is more often used
in modern mathematics to refer to the base of
a number system, such as the base 2 in the
binary system. However, the word "radical" is
retained with its original meaning of "root."
The radical symbol 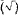 appears to be a
distortion of the initial letter "r" from the word "radix."
With long usage, the r gradually lost its
significance as a letter and became distorted into the symbol as we use it. The
vinculum helps to specify exactly which of the letters
and numbers following the radical sign actually
belong to the radical expression. appears to be a
distortion of the initial letter "r" from the word "radix."
With long usage, the r gradually lost its
significance as a letter and became distorted into the symbol as we use it. The
vinculum helps to specify exactly which of the letters
and numbers following the radical sign actually
belong to the radical expression.
The number under a radical sign is the RADICAND. The index of the root
(except in the case of a square root) appears
in the trough of the radical sign. The index
tells what root of the radicand is intended.
For example, in  , the
radicand is 32 and the index of the root is 5. The
fifth root of 32 is intended. In , the
radicand is 32 and the index of the root is 5. The
fifth root of 32 is intended. In 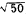 , the square
root of 50 is intended. When the index is 2,
it is not written, but is understood. , the square
root of 50 is intended. When the index is 2,
it is not written, but is understood.
If we can find one square root of a number we
can always find two of them. Remember (3)2
is 9 and (-3)2 is also 9. Likewise (4)2 and (-4)2
both equal 16 and (5)2 and (-5)2 both equal 25.
Conversely, 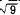 is +3 or -3, is +3 or -3, 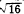 is +4 or -4, and
is +4 or -4, and  is +5 or -5. When we wish to show a number
that may be either positive or negative, we may use the symbol + which is read
"plus or minus." Thus
3 means "plus or minus 3." Usually
when a number is placed under the radical
sign, only its positive root is desired and,
unless otherwise specified, it is the only
root that need be found.
is +5 or -5. When we wish to show a number
that may be either positive or negative, we may use the symbol + which is read
"plus or minus." Thus
3 means "plus or minus 3." Usually
when a number is placed under the radical
sign, only its positive root is desired and,
unless otherwise specified, it is the only
root that need be found.
COMBINING RADICALS
A number written in front of another number and
intended as a multiplier is called a COEFFICIENT. The expression 5x means 5
times x; means a times y; and 7 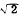 means 7 times
means 7 times 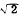 .
In these examples, 5 is the coefficient of x,
a is the coefficient of y, and 7 is the coefficient of .
In these examples, 5 is the coefficient of x,
a is the coefficient of y, and 7 is the coefficient of 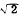 . .
Radicals having the same index and the same radicand
are SIMILAR. Similar radicals may have
different coefficients in front of the radical sign. For example, 3 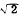 , ,
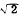 , and 1/5 , and 1/5 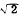 are similar radicals. When a coefficient is not
written, it is understood to be 1. Thus, the
coefficient of
are similar radicals. When a coefficient is not
written, it is understood to be 1. Thus, the
coefficient of 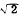 is 1. The rule for adding
radicals is the same as that stated for adding denominate numbers: Add only
units of the same kind. For example, we could
add 2 is 1. The rule for adding
radicals is the same as that stated for adding denominate numbers: Add only
units of the same kind. For example, we could
add 2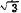 and 4 and 4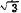 because the "unit" in each of these numbers is the same (
because the "unit" in each of these numbers is the same (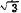 ).
By the same reasoning, we could not add 2 ).
By the same reasoning, we could not add 2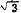 and 4
and 4 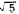 because these are
not similar radicals. because these are
not similar radicals.
Addition and Subtraction
When addition or subtraction of similar radicals is indicated, the radicals
are combined by adding or subtracting their
coefficients and placing the result in front
of the radical. Adding 3 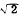 and 5 and 5 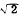 is similar to adding 3 bolts and 5 bolts. The
following examples illustrate the addition
and subtraction of similar radical expressions:
is similar to adding 3 bolts and 5 bolts. The
following examples illustrate the addition
and subtraction of similar radical expressions:
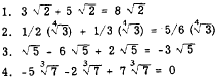
Example 4 illustrates a case that is sometimes troublesome. The sum of the
coefficients, -5, -2, and 7, is 0. Therefore,
the coefficient of the answer would be 0, as
follows:
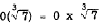
Thus the final answer is 0, since 0 multiplied by
any quantity is still 0.
Practice problems. Perform the indicated operations:
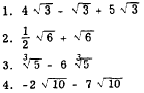
Answers

|











