|
POSITIONING NUMBERS ON THE K SCALE.-
Since a given number can be located in three positions
on the K scale,
the question arises as to which third of the
K scale to use when locating a number. Generally, the left index, the left
middle index, the right middle index, and the
right index are considered to be numbered as
shown in figure 8-7.
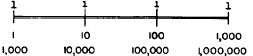
Figure 8-7.-Powers of 10 associated with K-scale
indices.
A system similar to that used with square roots
may be used to locate the position of a number
on the K scale. Groups of three are used
rather than groups of two. The grouping for
cube root is illustrated as follows:

For whole or mixed numbers the following rules
apply:
1. If the left-hand group contains one digit, locate
the number in the left third of the K scale.
2. If the left group contains two digits, locate the number in the middle
third of the K scale.
3. If the left group contains three digits, locate
the number in the right third of the K scale.
The following examples illustrate the foregoing rules:
1. 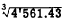
(One digit)-left third K scale.
2. 
(Two digits)-middle third K scale.
3. 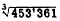
(Three digits)-right third of K scale.
For positive numbers less than one, look from
left to right and find the first group that contains
a digit other than zero.
1. If the first two figures in this group are zeros,
locate the number in the left third of the K
scale.
2. If only the first figure in this group is zero,
locate the number in the middle third of the
K scale.
3. If the first figure of the group is not zero, locate
the number in the right third of the K
scale.
The following examples illustrate these rules:
1. 
(Two zeros)-left third K scale.
2. 
(One zero)-middle third K scale.
3. 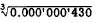
(No zero)-right third K scale.
PLACING THE DECIMAL POINT.-To place the
decimal point in the cube root of a number, we
use the system of marking off in groups of three
as shown above.
For whole or mixed numbers, there is one digit
in the root to the left of the decimal point for
every group marked in the original number. Thus,
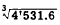
(Two digits in root to left of decimal point.)
For positive numbers less than one, there will
be one zero in the root between the decimal point
and the first significant digit for every three
zeros counted between the decimal point and
the first significant digit of the original number.
Thus,

(Two zeros between decimal point and first significant digit of root.)
EXAMPLE: 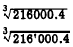
(Three digits in left group)
Place the hairline over 216 in the right third of the
K scale. Read the digit sequence, 6, under the
hairline on the D scale. Since there are two
groups in the original number, there are two
digits to the left of the decimal point in the root.
Thus,
EXAMPLE: 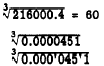
(Only first figure is
zero in this group)
Place the hairline over 451 in the middle third of
the K scale.
Read the digit sequence, 357, under the
hairline on the D scale. Since there is one
group of three zeros, there is one zero between
the decimal point and the first significant digit of the root. Thus,
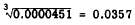
POWERS OF 10.-To take the cube root of a power
of 10, mark it off as explained in the preceding
paragraphs. The number in the left group will
then be 1, 10, or 100. We know that the cube
root of 10 is a number between 2 and 3. Thus,
for the cube root of any number whose left
group is 10, use the K scale index which lies
between 2 and 3 on the D scale. The cube root
of 100 lies between 4 and 5. Therefore, for a
number whose left group is 100, use the K scale
index between 4 and 5 on the D scale.
Practice problems. Following are some problems
and the digit sequence (d. 6.) of the roots.
Locate the decimal point for each root.
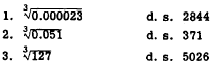

Answers:
1. 0.02844
2. 0.371
3. 5.026
4. 58.9
5. 902
6. 17
|







