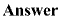CONVERSION TO DECIMAL

Computer data will have little meaning to you if you are not familiar with the various number systems. It is often necessary to convert those binary, octal, or hex numbers to decimal numbers. The need for understanding is better illustrated by showing you a paycheck printed in binary. A check in the amount of $10,010,101.00₂ looks impressive but in reality only amounts to $149.00₁₀.

Binary to Decimal

The computer that calculates your pay probably operates with binary numbers, so a conversion takes place in the computer before the amount is printed on your check. Some computers, however, don't automatically convert from binary to decimal. There may be times when you must convert mathematically.

To convert a base 2 number to base 10, you must know the decimal equivalent of each power of 2. The decimal value of a power of 2 is obtained by multiplying 2 by itself the number of times indicated by the exponent for whole numbers; for example, 2⁴ = 2 X 2 X 2 X 2 or 16₁₀.

For fractional numbers, the decimal value is equal to 1 divided by 2 multiplied by itself the number of times indicated by the exponent. Look at this example:

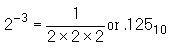
The table below shows a portion of the positions and decimal values of the binary system:

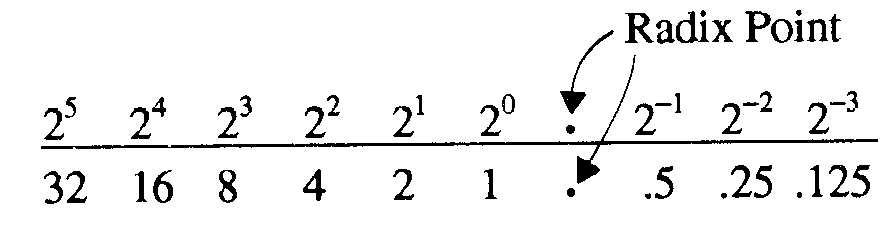
Remember, earlier in this chapter you learned that any number to the 0 power is equal to 1₁₀.

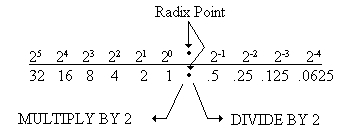
Another method of determining the decimal value of a position is to multiply the preceding value by 2 for whole numbers and to divide the preceding value by 2 for fractional numbers, as shown below:

Let's convert a binary number to decimal by using the positional notation method. First, write out the number to be converted; then, write in the decimal equivalent for each position with a 1 indicated. Add these values to determine the decimal equivalent of the binary number. Look at our example:

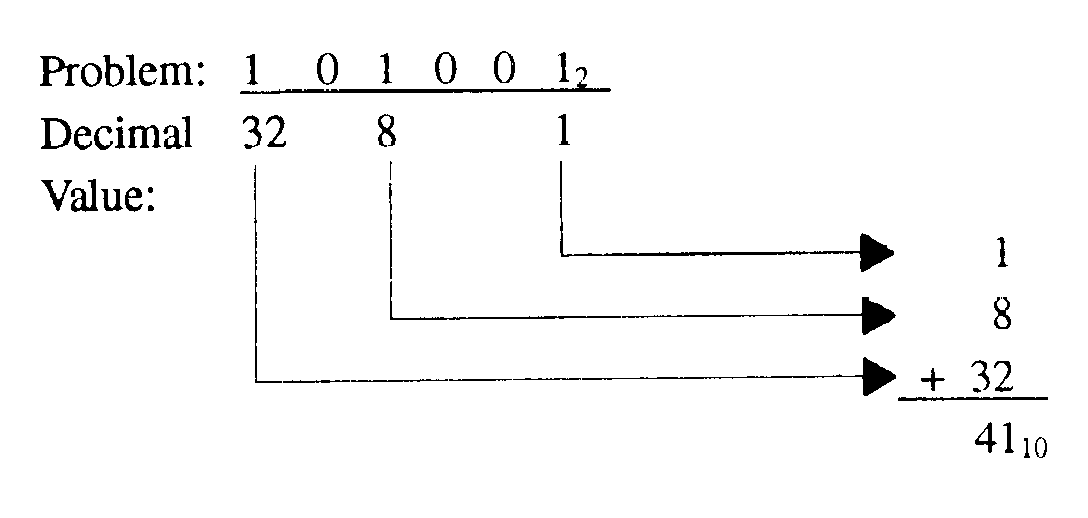
You may want to write the decimal equivalent for each position as we did in the following example. Add only the values indicated by a 1.

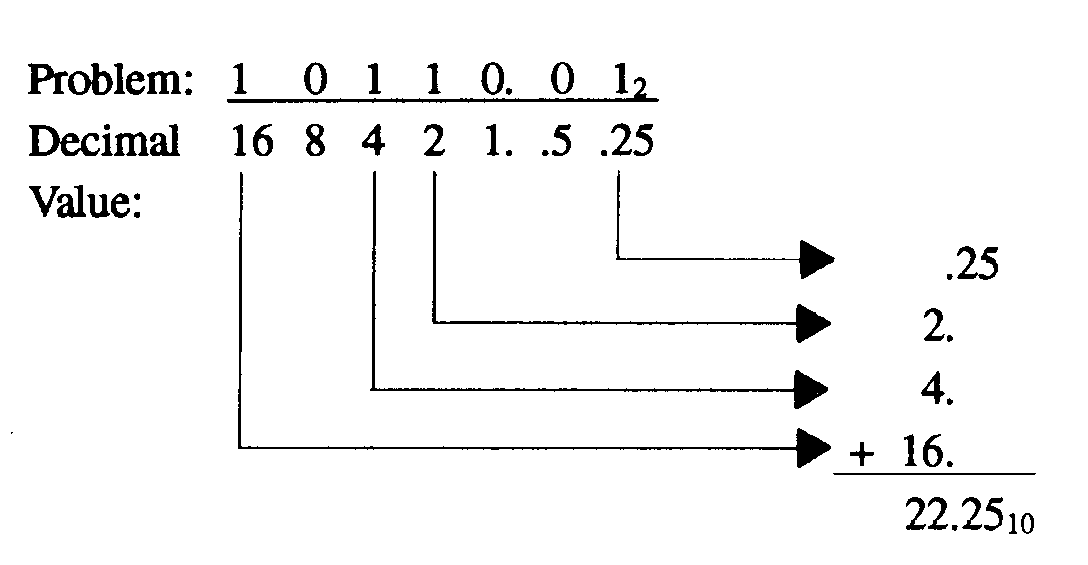
You should make sure that the decimal values for each position are properly aligned before adding. For practice let's convert these binary numbers to decimal:

Q.91 10010₂.
Q.92 1111100₂.
Q.93 1010101₂.
Q.94 0.0101₂.
Q.95 0.1010₂.
Q.96 1101101.1111₂.