Offshore location by chaining

Custom Search

Airfield surveys

Intermediate Engineering

Offshore location by triangulation

OFFSHORE LOCATION BY CHAINING
Figure 10-28 shows a situation in which offshore locations of piles for a wharf were determined by chaining. We will call each series of consecutive piles running offshore a line and each series running parallel to the shore a row. Alignment for each line was obtained by transitset up on a shore base line offset from the inboard row of piles. In each line the distance from one pile to the next was chained, as shown.

In figure 10-28 the lines are perpendicular to the base line, which means that the angle turned from the base line was 90 and the distance from one transit setup to the next was the same as the prescribed distance between lines. If the lines were not perpendicular to the base line, both the angle turned from the base line, the distance from one transit setup to the next, and the distance from the base line to the first offshore pile in each line would have to be determined.

Consider figure 10-29, for example. Here the angle between each line and the base line (either as prescribed or as measured by protractor on a plan) is 6040. You can determine the distance between transit setups by solving the triangle JAB for AB, JA being drawn from transit setup B perpendicular to the

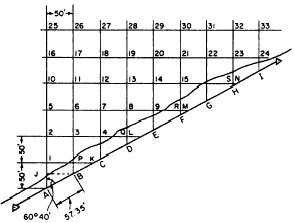
Figure 10-29.Offshore location in line oblique to the base line.

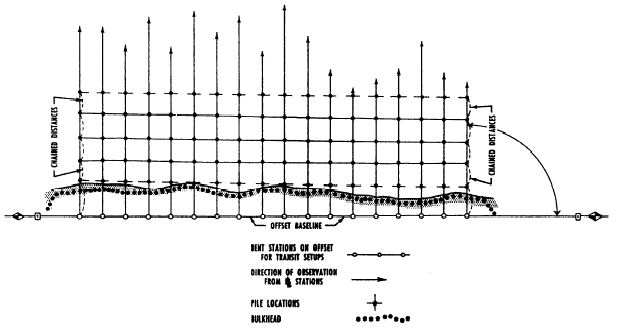
Figure 10-28.Offshore location by chaining

line from transit setup A through piles 1, 2, 5, 10, 16, and 25. AB measures 50/sin 6040, or 57.35 feet. This, then, is the distance between adjacent transit setups on the base line.

The distance from the base line to the first offshore pile in any line also may be determined by right-triangle solution. For pile No. 1 this distance is prescribed as 50 feet. For piles 2, 3, and 4, first solve the triangle A2L for 2L, which is 100/tan 2920, or 177.95 feet. The distance from 2 to Q is 150 feet; therefore, QL measures 177.95 150, or 27.95 feet. QD amounts to 27.95/tan 6040, or 15.71 feet. Therefore, the distance from transit setup D to pile No. 8 is 50 + 15.71, or 65.71 feet. Knowing the length of QL and the distance from setup point B to pile No. 3 by solving the right triangle LB3 for B3.

You can determine the distance E9 by solving the right triangle M5A and proceeding as before. You can determine the distance F15, G22, and H23 by solving the right triangle AN10 and proceeding as before. For pile No. 24, the distance I24 amounts to 50 tan 2920, or 28.10 feet.