What is the corresponding horizontal distance? You read the graduation indicated by the Beaman arc indicator on the H scale, and find that the reading is 5. This means that the horizontal distance is 5 percent less than the slope distance, or

245 feet (0.05 x 245 feet), or

Difference in Elevation (Vertical Index at 50). The V scale on the Beaman arc is used to determine the difference in elevation between the elevation of the line of sight through the telescope (that is, the HI) and the elevation of the point you sighted on the level rod Note that when the telescope is horizontal, the V scale on the Beaman arc reads 50. This arrangement makes the use of minus values unnecessary when you are sighting with the telescope at a negative vertical angle.

To read the V scale, you take the difference between 50 and whatever you read on the scale and apply this difference as follows to determine the difference in elevation.

Suppose that when you made the shot previously described (where you read 5 on the H scale), the reading V scale was 71. In practice, it is the custom to V scale.

Figure 8-9 shows two situations that are encountered in transit-stadia work First, let us discuss the common situation in which you desire to determine the difference in elevation between an instrument station of known elevation and a ground point of unknown elevation. This situation is shown in figure 8-9, view A. In this view, the elevation of the instrument station P is known and it is desired to determine the difference in elevation between P and the rod station P₁. The horizontal center-line height of the instrument (h.i.) above point P is equal to PA. As you can see, this h.i. is different than the HI that you are accustomed to working with indirect leveling. The rod reading is P₁B.

From your studies, you know that the difference in elevation (DE) between P and P1 can be expressed as follows:

Therefore, the ground elevation at P₁ can be expressed as follows:

Now let us sight on the rod such that P₁B = PA = h.i. In (PC₁P₁) is formed at the instrument station P. From observation of these similar triangles, you can see that the DE= P₁C₁ = BC. Therefore, the ground elevation at P₁ can be simply expressed as follows:

Figure 8-9.-Difference in elevation.

you can see, when the center cross hair is sighted on a rod graduation that is equal to the h.i. before reading the vertical angle, then calculating the difference in elevation is greatly simplified. Obviously, though, if the line of sight is obstructed and you cannot sight on a rod graduation that is equal to the hi., then you must sight on some other graduation.

Another, although less frequent, occurrence in topographic work using stadia is shown in figure 8-9, view B. In this situation it is desired to determine the difference in elevation between two points on the ground (P1 and P2) from an instrument station (E) that is located between the two points.

For this discussion, let us assume that a backsight is taken on a rod held at P₁ and then a foresight is taken to P₂. Now the difference in elevation (DE) between the two points can be written as follows:

In reverse, if a backsight was taken to P₂ with a foresight P₁, then the expression for DE can be written as follows:

Figure 8-10.-Notes for locating topographical details by transit and stadia.

Now let us see how all that you have learned about transit-stadia topography is used in the field Figure 8-10 shows field notes for locating topographic details by transit and stadia. The details shown by numbers in the sketch on the Remarks side are listed on the data side by numbers in the column headed Obj. At the top of the page on the data side, you see that control point D1 was used as the instrument station. Immediately below this, you see that from instrument-station D1, the transit was backsighted to point A and that all horizontal angles were measured to the right from the backsight on A. In the third line from the top on the data side, you see that the known elevation of D1 is 532.4 feet and that the vertical distance (hi.) from the point or marker at D1 to the center of the instrument above D1 is 4.8 feet. This vertical distance was carefully determined by measurement with a tape or rod held next to the instrument.

Now let us see how each of the objective points was detailed. We will begin with point 1. Remember that in this example, D1 is the instrument station from which all observations are made.

To determine the direction of point 1, train the transit telescope on A and match the zeros. Next turn the telescope right to train on point 1 and read the horizontal angle (30010).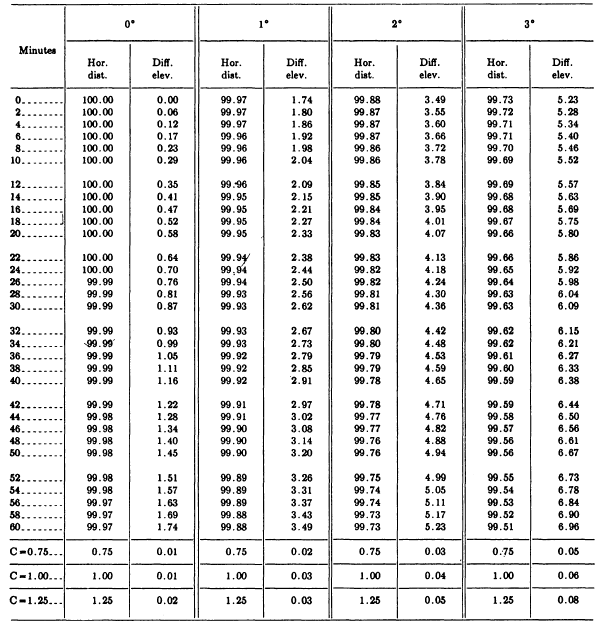

Figure 8-11.-Horizontal distances and elevations from stadia readings.

For the horizontal distance and elevation of point 1, set a rod on the point, and train the lower stadia hair of the transit telescope on a whole-foot mark on the rod so that the center hair is near the 4.8 graduation. (This is a common practice in stadia work that makes reading the stadia interval easier.) Then read and record the stadia interval (in this case 6.23 feet). Next, rotate the telescope about the horizontal axis until the center hair is on the 4.8 rod graduation. Lock the vertical motion and read and record the vertical angle (-3026). Be sure to record each vertical angle correctly as plus or minus. While you are reading and recording the vertical angle, the rodman can be moving to the next point. This will help speed up the survey.

From the stadia interval and the vertical angle reading, the horizontal distance (entered in the fifth column of fig. 8-10) and the difference in elevation (in the sixth column) are determined from a stadia reduction table. Figure 8-11 shows the page from a stadia reduction table that applies to the data for point 1 in figure 8-10. For this point, the vertical angle is 326, and the stadia interval is 6.23 feet. In the table under 3 and opposite 26, note that the multiplier for horizontal distance is 99.64, while the one for difference in elevation is 5.98. If the final distance is ignored, the horizontal distance is

To these figures, add the corrections for focal distance given at the bottom of the page. For an instrument with a focal distance of 1 foot, add 1 foot to the horizontal difference (making a total horizontal distance of 622 feet) and 0.06 foot to the difference in elevation This makes the difference in elevation round off to 37.4 feet; and since the vertical angle has a negative (-) sign, the difference in elevation is recorded as 37.4 feet. In the first column on the Remarks side of figure 8-10, enter the elevation of each point, computed as follows. For point 1, the elevation equals the elevation of instrument station D1 (532.4 feet) minus the difference in elevation (37.4 feet), or 495.0 feet.

The remainder of the points in this example were detailed in a similar reamer except for point 13. When a detail point is at the same, or nearly the same, elevation as the instrument station, the elevation can be determined more readily by direct leveling. That was the case for point 13. As seen in the vertical-angle column of the notes, the vertical angle was 0 at a rod reading of 5.6 feet. Therefore the elevation of point 13 is equal to the elevation of the instrument station (532.4 feet) plus the h.i. (4.8 feet) minus the rod reading (5.6 feet), or 531.6 feet.

In the above example, as you recall, the transit was initially backsighted to point A and the zeros were matched This was because the azimuth of D1A was not known. However, if you knew the azimuth of D1A, you could indicate your directions in azimuths instead of in angles right from D1A. Suppose, for example, that the azimuth of D1A was Train the telescope on A and set the horizontal limb to read Then when you train on any detail point, read the azimuth of the line from D1 to the detail point.