|
Surface Area and Volume
The lateral area of a cylinder is the area of its
curved surface, excluding the area of its bases.
Figure 18-15 illustrates an experimental method of determining the lateral area
of a right circular cylinder.
The card of length L and width W in figure 18-15
is rolled into a cylinder. The height of the
cylinder is W and the circumference is L. The
lateral area is the same as the original area
of the card, LW. Therefore, the lateral area
of the cylinder is found by multiplying its height
by the circumference of its base. Written
as a formula, this is
A = Ch
EXAMPLE: Find the lateral area of a right circular
cylinder whose base has a radius of 4
inches and whose height is 6 inches.
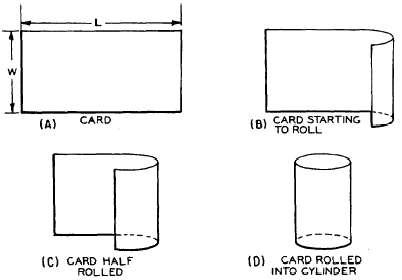
Figure 18-15.-Lateral area of a cylinder.
SOLUTION: The circumference of the base is

Therefore,
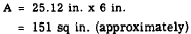
The formula for the volume of a cylinder is obtained
by the same reasoning process that was used
for prisms. The cylinder is considered to be composed of many circular wafers,
or disks, each one unit thick. The area of each
disk, multiplied by the number of disks, is the
volume of the cylinder. With V representing volume,
A drepresenting the area of each disk, and n
representing the number of disks, the formula
is as follows:
V = Adn
Since the number of disks is the same as the height
of the cylinder, the formula for the volume of a cylinder is normally written
V = Bh
In this formula, B is the area of the base and h
is the height of the cylinder.
EXAMPLE: Determine the volume of a circular cylinder
with a base of radius 5 inches and a height
of 14 inches.
SOLUTION:
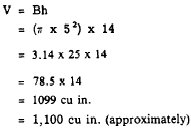
Practice problems:
1. Determine the lateral area of a right circular cylinder
with a base of diameter 7 inches and
a height of 4 inches.
2. Determine the volume of the cylinder in problem
1.
Answers:
1. 88 sq in.
2. 154 cu in.
|

|

