RADICALS

To differentiate a function containing a radical, replace the radical by a fractional exponent; then find the derivative by applying the appropriate theorems.

EXAMPLE. Find the derivative of

SOLUTION: Replace the radical by the proper fractional exponent, such that

and by Theorem 6

EXAMPLE: Find the derivative of

SOL UTION: Replace the radical by the proper fractional exponent, thus

At this point a decision is in order. This problem may be solved by either writing

and applying Theorem 6 in the denominator and then applying Theorem 5 for the quotient or writing

and applying Theorem 6 for the second factor and then applying Theorem 4 for the product.

The two methods of solution are completed individually as follows:

Use equation (1):

Find the derivative of the denominator

by applying the power theorem

The derivative of the numerator is

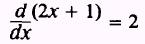
Now apply Theorem 5:

Multiply both numerator and denominator by

and simplify:

To find the same solution by a different method, use equation (2):

Find the derivative of each factor:

and

Now apply Theorem 4:

Multiply both numerator and denominator by

such that,

which agrees with the solution of the first method used.

PRACTICE PROBLEMS:

Find the derivatives of the following:

ANSWERS: