INVERSE FUNCTIONS

Theorem 7. The derivative of an inverse function is equal to the reciprocal of the derivative of the direct function.

In the equations to this point, x has been the independent variable and y has been the dependent variable. The equations have been in a form such as

Suppose that we have a function like

and we wish to find the derivative . Notice that if we solve for y in terms of x, using the quadratic formula, we get the more complicated function:

if we call this function the direct function, then

is the inverse function. To determine from the inverse

function is easy.

EXAMPLE: Find the derivative of the function

SOLUTION.The derivative is

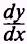The reciprocal of is the derivative of the direct function, and we find

EXAMPLE: Find the derivative of the function

SOL UTION.^- Find to be

Then

PRACTICE PROBLEMS:

Find the derivative of the following functions:

ANSWERS: