TRIGONOMETRIC FUNCTIONS

Trigonometric functions, which comprise one group of transcendental functions, may be differentiated and integrated in the same fashion as the other functions. We will limit our proofs to the sine, cosine, and secant functions but will list several others.

Formula.

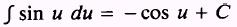
PROOF:

and

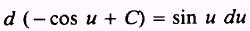
Therefore,

Formula.

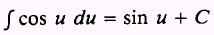
PROOF:

Therefore,

Formula.

PROOF:

and by the quotient rule

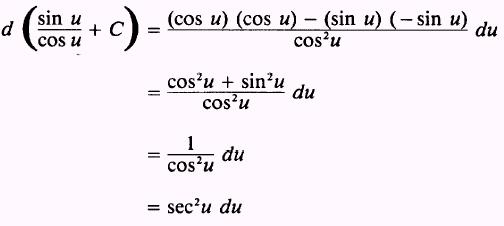
Therefore,

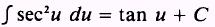
To this point we have considered integrals of trigonometric functions that result in functions of the sine, cosine, and tangent. Those integrals that result in functions of the cotangent, secant, and cosecant are included in the following list of elementary integrals:

EXAMPLE: Evaluate

SOLUTION: We need the integral in the form of

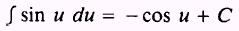
We let

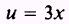
so that

but we do not have 3 dx. Therefore, we multiply the integral by 3/3 and rearrange as follows:

EXAMPLE: Evaluate

SOLUTION: Let

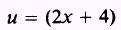
so that

Therefore,

EXAMPLE: Evaluate

SOLUTION: We use the rule for sums and write

Then, in the integral

let

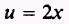
so that

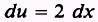
but we have

3 dx

Hence, proper compensation has to be made as follows:

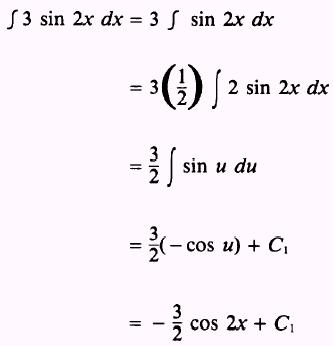
The second integral

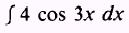
with

and

is evaluated as follows:

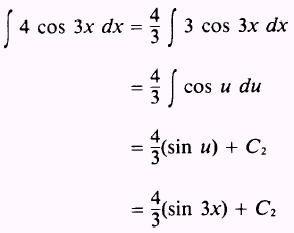
Then, by combining the two solutions, we have

where

EXAMPLE: Evaluate

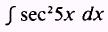
SOL UTION: Let

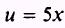
so that

We need 5 dx so we write

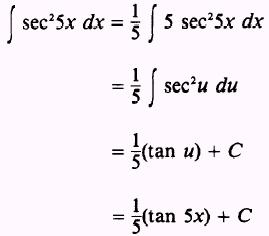
EXAMPLE: Evaluate

SOL UTION: Let

so that

We require du equal to 2 dx, so we write

EXAMPLE: Evaluate

SOL UTION: Let

u=6x

so that

then,

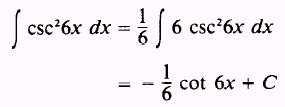
EXAMPLE: Evaluate

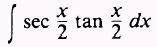
SOL UTION: Let

so that

then,