|
This chapter will cover the
measure of angles in terms of radians and degrees. EO 1.4 STATE the definition of a radian.
Radian Measure
The size of an angle is usually measured in degrees.
However, in some applications the size of an angle is measured in radians. A
radian is defined in terms of the length of an arc subtended by an angle at the
center of a circle. An angle whose size is one radian subtends an arc whose
length equals the radius of the circle. Figure 4 shows  BAC
whose size is one radian. The length of arc BC equals the radius r of the circle. The size of an angle, in radians, equals
the length of the arc it subtends divided by the radius. BAC
whose size is one radian. The length of arc BC equals the radius r of the circle. The size of an angle, in radians, equals
the length of the arc it subtends divided by the radius.
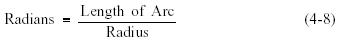
One radian equals approximately 57.3 degrees. There are
exactly 2 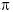 radians in a complete revolution. Thus 2 radians in a complete revolution. Thus 2 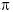 radians equals 360 degrees: radians equals 360 degrees: 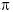 radians equals 180 degrees. radians equals 180 degrees.
Although the radian is defined in terms of the length of
an arc, it can be used to measure any angle. Radian measure and degree measure
can be converted directly. The size of an angle in degrees is changed to
radians by multiplying by 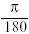 . The size of an angle in radians is changed to
degrees by multiplying by . The size of an angle in radians is changed to
degrees by multiplying by 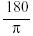 . .
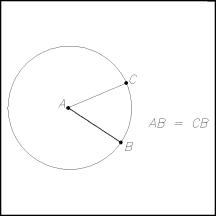
Figure 4 Radian
Angle
Example:
Change 68.6 to radians.
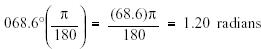
Example:
Change
1.508 radians to degrees.
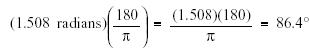
Summary
The
important information in this chapter is summarized below.
Radian
Measure Summary
A
radian equals approximately 57.3 and is defined as the angle subtended by an
arc whose length is equal to the radius of the circle.
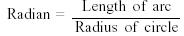
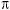 radians = 180 radians = 180
|







