Using Determinant

Square matrixes have a property called a determinant. When a determinant of a matrix is written, it is symbolized by vertical bars rather than brackets around the numbers. This differentiates the determinant from a matrix. The determinant of a matrix is the reduction of the matrix to a single scalar number. The determinant of a matrix is found by "expanding" the matrix. There are several methods of "expanding" a matrix and calculating it's determinant. In this lesson, we will only look at a method called "expansion by minors."

Before a large matrix determinant can be calculated, we must learn how to calculate the determinant of a 2 x 2 matrix. By definition, the determinant of a 2 x 2 matrix is calculated as follows:

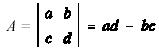
Example: Find the determinant of A.

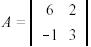
Solution:

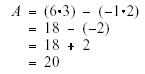
To expand a matrix larger than a 2 x 2 requires that it be simplified down to several 2 x 2 matrices, which can then be solved for their determinant. It is easiest to explain the process by example.

Given the 3 x 3 matrix:

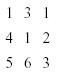
Any single row or column is picked. In this example, column one is selected. The matrix will be expanded using the elements from the first column. Each of the elements in the selected column will be multiplied by its minor starting with the first element in the column (1). A line is then drawn through all the elements in the same row and column as 1. Since this is a 3 x 3 matrix, that leaves a minor or 2 x 2 determinant. This resulting 2 x 2 determinant is called the minor of the element in the first row first column.

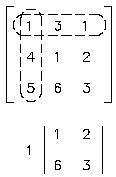
The minor of element 4 is:

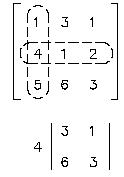
The minor of element 5 is:

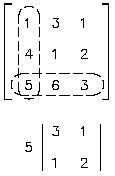
Each element is given a sign based on its position in the original determinant.

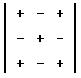
The sign is positive (negative) if the sum of the row plus the column for the element is even (odd). This pattern can be expanded or reduced to any size determinant. The positive and negative signs are just alternated.

Each minor is now multiplied by its signed element and the determinant of the resulting 2 x 2 calculated.

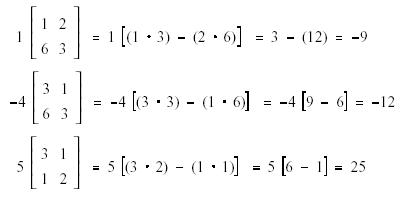
Determinant = (-9) + (-12) + 25 = 4

Example:

Find the determinant of the following 3 x 3 matrix, expanding about row 1.

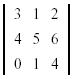
Solution: