Matrices and their determinant can be used to solve a system of equations. This method becomes especially attractive when large numbers of unknowns are involved. But the method is still useful in solving algebraic equations containing two and three unknowns.

In part one of this chapter, it was shown that equations could be organized such that their coefficients could be written as a matrix.

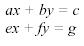
where:

x and y are variables

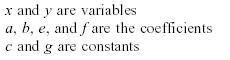
The equations can be rewritten in matrix form as follows:

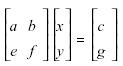
To solve for each variable, the matrix containing the constants (c,g) is substituted in place of the column containing the coefficients of the variable that we want to solve for (a,e or b f ). This new matrix is divided by the original coefficient matrix. This process is call "Cramer's Rule."

Example:

In the above problem to solve for x,

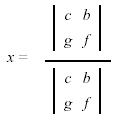
and to solve for y,

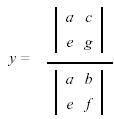
Example:

Solve the following two equations:
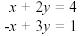