A curve that is made up of a series of successive tangent circular arcs is called a compound curve. In figure 4-40 the problem is to construct a compound curve passing through given points A, B, C, D, and E. First, connect the points by straight lines. The straight line between each pair of points constitutes the chord of the arc through the points.

Erect a perpendicular bisector from AB. Select an appropriate point 0₁ on the bisector as a center, and draw the arc AB. From 0₁, draw the radius 0₁B. From BC, erect a perpendicular bisector. The point of intersection 0₂ between this bisector and the radius 0₁B is the center for the arc BC. Draw the radius 0₂C, and erect a perpendicular bisector from CD. The point of intersection 0₃ of this bisector and the extension of 0₂C is the center for the arc CD. 

To continue the curve from D to E, you must reverse the direction of curvature. Draw the radius 0₃D, and erect a perpendicular bisector from DE on the opposite side of the curve from those previously erected. The point of intersection of this bisector and the extension of 0₃D is the center of the arc DE.

A reverse, or ogee, curve is composed of two consecutive tangent circular arcs that curve in opposite directions,

Figure 4-41 shows a method of connecting two parallel lines by a reverse curve tangent to the lines. The problem is to construct a reverse curve tangent to the upper line at A and to the lower line at B.

Connect A and B by a straight line AB. Select on AB point C where you want to have the reverse curve change direction. Erect perpendicular bisectors from BC and CA, and erect perpendiculars from B and A. The points of inter-section between the perpendiculars (0₁ and 0₂) are the centers for the arcs BC and CA.

Figure 4-42 shows a method of constructing a reverse curve tangent to three intersecting straight lines. The problem is to draw a reverse

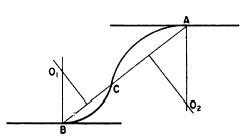
Figure 4-41.Reverse curve connecting and tangent to two parallel lines.

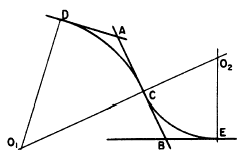
Figure 4-42.Reverse curve tangent to three intersecting straight lines.

curve tangent to the three lines that intersect at points A and B. Select on AB point C where you want the reverse curve to change direction. Lay off from A a distance equal to AC to establish point D. Erect a perpendicular from D and another from C. The point of intersection of these perpendiculars (0₁) is the center of the arc DC.

Lay off from B a distance equal to CB to establish point E. Erect a perpendicular from E, and extend 0₁C to intersect it. The point of intersection (0₂) is the center of the arc CE.