|
CIRCULAR ARC OF A GIVEN RADIUS TANGENT
TO A STRAIGHT LINE AND TO
ANOTHER CIRCULAR ARC The problem in figure 4-35 is to draw a
circular arc with a radius equal to AB, tangent
to the circular arc CD and to the straight line EF.
Set a compass to a radius equal to the radius of
the circular arc CD plus the given radius AB
(which is indicated by the dashed line shown),
and, with O as a center, strike the arc GH. Draw
a line IJ parallel to EF at a distance from EF equal
to AB. The point of intersection (P) between GH
and IJ is the center of the circle of which an arc
of the given radius is tangent to CD and EF.
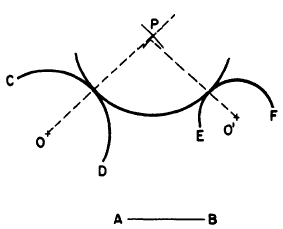
Figure 4-36.-Circular arc tangent to two other circular
arcs.
CIRCULAR ARC OF A GIVEN
RADIUS TANGENT TO TWO
OTHER CIRCULAR ARCS
The problem in figure 4-36 is to draw an arc
with a radius equal to AB, tangent to the circular
arcs CD and EF. Set a compass to a spread equal
to the radius of arc CD plus AB (indicated by the
left-hand dashed line), and, with O as a center,
strike an arc. Set the compass to a spread equal
to the radius of arc EF plus AB (indicated by the
right-hand dashed line), and, with O as a center,
strike an intersecting arc. The point of inter-section
between the two arcs (P) is the center of
the circle of which an arc of given radius is tangent
to arcs CD and EF.
In figure 4-36 the circular arcs CD and EF
curve in opposite
directions. In figure 4-37 the
problem is to draw an arc with radius equal to
AB, tangent to two circular arcs, CD and EF, that
curve in the same
direction.
Set a compass to a radius equal to the radius
of EF less AB, and, with O as a center, strike
an arc. Then, set a compass to a radius equal to
the radius of arc CD plus line AB, and, with O
as center, strike an intersecting arc at P. The point
of intersection of these two arcs is the center of
the circle of which an arc of the given radius is
tangent to CD and EF.
When a circular arc is tangent to another, it
is commonly the case that the two arcs curve in
opposite directions. However, an arc may be
drawn tangent to another with both curving in the
same direction. In a case of this kind, the tangent
arc is said to enclose the other.
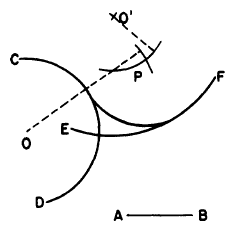
Figure 4-37.-Circular arc tangent to arcs that curve in the
same direction.
An arc tangent to two others may enclose both, or it may enclose only
one and not the other. In
figure 4-38 the problem is
to draw a circular arc with a radius equal
to AB, tangent to and enclosing both arcs
CD and EF. Set a compass to a radius
equal to AB less the radius of CD (indicated
by the dashed line from O), and, with O
as a center, strike an arc. Set the compass
to a radius equal to AB less the radius
of EF (indicated by the dashed line from
O), and, with O as a center, strike an inter-secting
arc at P. The point of intersection of
these two arcs is the center of a circle of which
an arc of given radius is tangent to, and encloses,
both arcs CD and EF.
In figure 4-39 the problem is to draw
a circular arc with a radius equal to AB,
tangent to, and enclosing, CD, and tangent
to, but NOT enclosing, EF. Set a compass
to a radius equal to AB less the radius
of arc CD (indicated by the dashed line from
0), and, with O as a center, strike an
arc, Set the compass to AB plus the radius
of EF (as indicated by the dashed line from
O), and, with O as a center, strike an inter-secting
arc at P. The point of intersection of the
two arcs is the center of a circle of which an arc
of the given radius is tangent to and encloses arc
CD and also is tangent to, but does not enclose,
arc EF.
Figure 4-38.-Circular arc tangent to and enclosing two other circular
arcs.
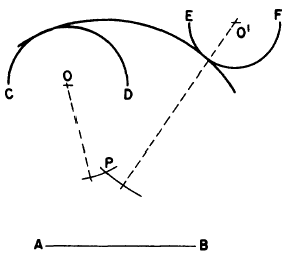
Figure 4-39.-Circular arc tangent to and enclosing one arc
and tangent to, but not enclosing, another.
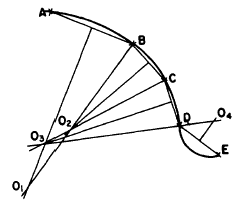
Figure 4-40.-Curve composed of a series of consecutive
tangent circular arcs.
|
|

