|
RECORDING NOTES FOR SLOPE
CHAINING. Figure 12-17
shows an example of slope chaining notes. Notice that on the data page, extra columns have been assigned for the
temperature of the tape at each interval, the difference in elevation between supports, and the
slope distance. Under "Tape Corr." in the fifth column, the standard error for each interval is entered. Again,
the tape had a standard error of 0.013 ft per 100 ft; therefore, the standard error for each interval
except the last is 0.013 ft. For the last interval of 73.18 ft, the error works out as 0.009 ft.
If you will look to the right of the "Tape Corr." column, you will see the "Temp.
Corr."
column. For the first two intervals measured, the temperature of the tape was 78F, or 10F above
standard. The correction amounts to 0.01 ft for each 15F above standard; therefore, the total
temperature correction for each of these intervals equals the value of x in the equation
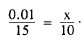
The total temperature correction is 0.007 ft. Because the temperature was above standard, the
tape lengthened and was reading short. So the
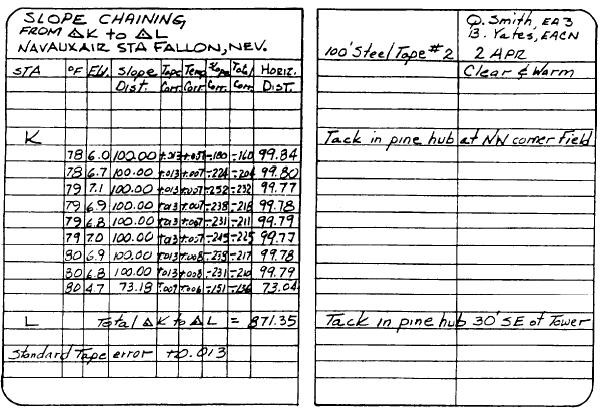
Figure 12-17.-Notes for slope
chaining.
corrections should be added as indicated by the
plus signs.
To the right of the "Temp. Corr." column
is the "Slope Corr." column. Its entries are to
be subtracted as indicated. Use the following
equation to compute the slope correction.
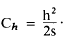
For the first taped interval, we have an h of 6.0
ft and an s of 100 ft.
Therefore
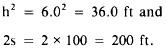
The slope correction is computed as follows:
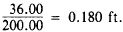
Next to the column for slope correction comes the
"Total Corr." column, containing the algebraic
sum of the three corrections for each taped
interval. Finally, in the "Horiz. Dist." column,
each value is determined by subtracting the total
correction for each interval from the measured
slope distance for that interval. (This example
used in figure 12-17 happens to be all negative.)
At the bottom of this column, the sum of the
horizontal distances appears. This is the
horizontal distance from station K to station L.
|

