In
laying out a right angle (or erecting a
perpendicular) by tape, you apply the basic trigonometric theory that a triangle with sides in the ratio of
3:4:5 is always a right triangle.
Assume that on the line AB shown in figure 12-18, you want to use a 100-ft tape to run a line
from C perpendicular to AB. If a triangle with sides in the ratio of 3:4:5 is a right triangle, then
one with sides in the ratio of 30:40:50 is also a right triangle. From C, measure off DC, 30 ft
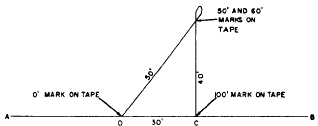
Figure 12-18.-Laying out a right angle using a 100-foot
tape.
long. Set the zero-foot end of the tape on D and
the 100-ft end on C. Have a person hold the 50-ft
and 60-ft marks on the tape together and run out
the bight. When the tape becomes taut, the 40-ft
length from C will be perpendicular to AB.
MEASURING AN ANGLE BY TAPE. There are two methods commonly used to
determine the size of an angle by tape: the
CHORD method and the TANGENT method.
The chord method can be applied, using the
example shown in figure 12-19. Suppose you want
to determine the size of angle A. Measure off
equal distances from A (80.0 ft), and establish
points B and C. Measure BC; assume that it
measures 39.5 ft, as shown. You can now
determine the size of angle A by applying the
following equation:
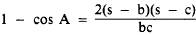
in which
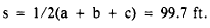
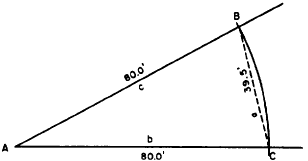
Figure 12-19.-Determining the size of an angle by the chord
method.
First, solving for
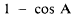
we have
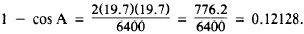
Since
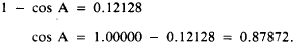
Reference to a table of natural functions shows
that the angle with cos equal to 0.87872 measures,
to the nearest 1 min., 2829.
The intervals measured off from A were made
equal for mere convenience. The solution will
work just as well for unequal intervals.
In determining the size of an angle by the
tangent method, you simply lay off a right triangle
and solve for angle A by the common tangent
solution.
Suppose that in figure 12-20, you want to
determine the size of angle A. Measure off AC
a convenient length (say, 80.0 ft). Lay off CB
perpendicular to AC and measure it; say it
measures 54.5 ft, as shown. The angle is computed
by using the following formula:
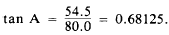
The angle with tangent 0.68125 measures 3418.
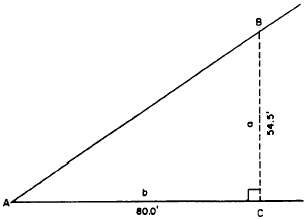
Figure 12-20.-Determining the size of an angle by the

