CONSTANT TO A VARIABLE POWER

In this section a discussion of two forms of a constant to a variable power is presented. The two forms are , where u is a variable, a is any constant, and e is a defined constant.

Formula.

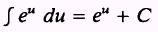
PROOF:

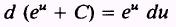
Therefore,

EXAMPLE: Evaluate

SOL UTION: Let

so that

The integral is in the correct form to use

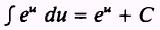
therefore, using substitution, we find

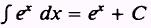
EXAMPLE: Evaluate

SOL UTION: Let

so that

We need a factor of 2 in the integral so that

EXAMPLE: Evaluate

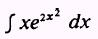
SOL UTION: Let

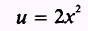
so that

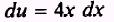
Here a factor of 4 is needed in the integral; therefore,

EXAMPLE: Evaluate

SOLUTION:

Let

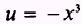
so that

Therefore,

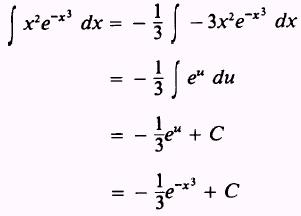
PRACTICE PROBLEMS: Evaluate the following integrals: 1. J - 2xe x2 dx

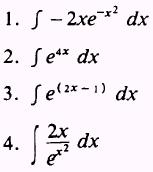
ANSWERS:

We will now discuss the second form of the integral of a constant to a variable power.

Formula.
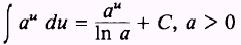